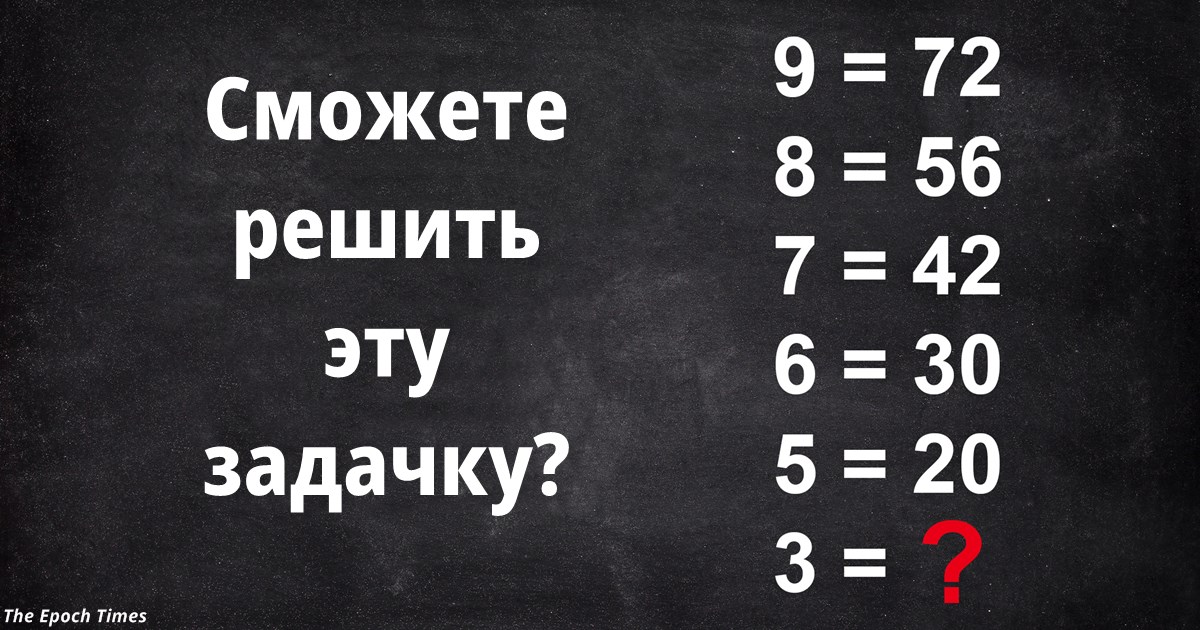В интернете появилась очередная математическая головоломка, которая не даёт людям покоя. На первый взгляд всё очень просто: в левом столбце — обратный отсчёт от 9 до 3, в правом — числовые соответствия. Надо вписать недостающее.
Задача вызвала нешуточные баталии онлайн. Попробуйте решить её самостоятельно!
А теперь давайте посмотрим, какие могут быть варианты ответа.

Итак, некоторые люди обнаружили в правом столбце произведение умножения. Разгадка проста: умножить число слева на такое же число минус один: x(x−1), что даёт результат в правом столбце. Например, 9(8) = 72, 8(7) = 56 и т. д. Следуя этому правилу, мы получаем ответ 6: 3(2) = 6.
Всё? А вот и нет!
Другие люди нашли такой вариант решения: они обратили внимание на последовательную разницу между числами в правом столбце — 72 − 56, затем 56 − 42, затем 42 − 30 и т. д., что даёт уменьшающуюся разницу 16, затем 14, затем 12 и т. д. Каждое последующее число меньше на 2. В таком случае последний ответ должен быть 12.
Но и это ещё не всё! Есть и третий вариант решения!
В левом столбце можно увидеть понижающееся на 1 умножение: 9 × 8, затем 7 × 7, затем 6 × 5 и т. д. В таком случае ответ будет 9, потому что в конце получится 3 × 3 = 9.
Но может ли быть так, что один из трёх вариантов решения подходит лучше других?
Для начала посмотрим на последовательность в левом столбце. Каждое последующее число меньше предыдущего на 1 — кроме последней строчки, которая меньше на 2. Конечно, мы с лёгкостью можем вычислить, что пропущена строчка с числом 4.
Почему же пропущенная строчка столь важна? А вот почему: если мы применяем для решения любую из трёх вышеописанных последовательностей — x(x−1), уменьшающееся вычитание либо уменьшающееся умножение — то при добавлении строчки с 4 мы получаем одинаковый ответ во всех трёх вариантах! И этот ответ — 6.
Поэтому логично предположить, что пропущенная строчка подходит к любому варианту решения, а следовательно, правильный ответ таки 6.
Запутались? Попробуйте предложить эту головоломку друзьям!